https://blog.csdn.net/u013733326/article/details/79827273
1. 神经网络和深度学习 – 第二周作业 – 具有神经网络思维的Logistic回归
目标: 搭建一个能够【识别猫】 的简单的神经网络
引入的库:
import numpy as np
import matplotlib.pyplot as plt
import h5py
from lr_utils import load_dataset- numpy :是用Python进行科学计算的基本软件包。
- h5py:是与H5文件中存储的数据集进行交互的常用软件包。
- matplotlib:用于在Python中绘制图表。
- lr_utils :在本文的资料包里,一个加载资料包里面的数据的简单功能的库
加载数据
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = load_dataset()lr_utils.py 中load_dataset 代码解释:
train_set_x_orig :保存的是训练集里面的图像数据(本训练集有209张64×64的图像)。
train_set_y_orig :保存的是训练集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
test_set_x_orig :保存的是测试集里面的图像数据(本训练集有50张64×64的图像)。
test_set_y_orig : 保存的是测试集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
classes : 保存的是以bytes类型保存的两个字符串数据,数据为:[b’non-cat’ b’cat’]。
def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes查看数据集情况
#打印出当前的训练标签值
#使用np.squeeze的目的是压缩维度,【未压缩】train_set_y[:,index]的值为[1] , 【压缩后】np.squeeze(train_set_y[:,index])的值为1
#只有压缩后的值才能进行解码操作
print("y=" + str(train_set_y[:,index]) + ", it's a " + classes[np.squeeze(train_set_y[:,index])].decode("utf-8") + "' picture")
m_train = train_set_y.shape[1] #训练集里图片的数量。
m_test = test_set_y.shape[1] #测试集里图片的数量。
num_px = train_set_x_orig.shape[1] #训练、测试集里面的图片的宽度和高度(均为64x64)。
#现在看一看我们加载的东西的具体情况
print ("训练集的数量: m_train = " + str(m_train))
print ("测试集的数量 : m_test = " + str(m_test))
print ("每张图片的宽/高 : num_px = " + str(num_px))
print ("每张图片的大小 : (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("训练集_图片的维数 : " + str(train_set_x_orig.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集_图片的维数: " + str(test_set_x_orig.shape))
print ("测试集_标签的维数: " + str(test_set_y.shape))把数组变为209行的矩阵(因为训练集里有209张图片),但是懒得算列有多少,于是我就用-1告诉程序你帮我算,最后程序算出来时12288列,我再最后用一个T表示转置,这就变成了12288行,209列。测试集亦如此
#将训练集的维度降低并转置。
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
#将测试集的维度降低并转置。
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
print ("训练集降维最后的维度: " + str(train_set_x_flatten.shape))
print ("训练集_标签的维数 : " + str(train_set_y.shape))
print ("测试集降维之后的维度: " + str(test_set_x_flatten.shape))
print ("测试集_标签的维数 : " + str(test_set_y.shape))标准化我们的数据集
对于图片数据集,几乎可以将数据集的每一行除以255(像素通道的最大值),因为在RGB中不存在比255大的数据,所以我们可以放心的除以255,让标准化的数据位于[0,1]之间
train_set_x = train_set_x_flatten / 255
test_set_x = test_set_x_flatten / 255开始构建神经网络 (不使用框架内置函数)
非线性激活函数sigmoid的实现, 方便后续 使用 sigmoid(w ^ T x + b) 计算来做出预测值
def sigmoid(z):
"""
参数:
z - 任何大小的标量或numpy数组。
返回:
s - sigmoid(z)
"""
s = 1 / (1 + np.exp(-z))
return s
print("====================测试sigmoid====================")
print ("sigmoid(0) = " + str(sigmoid(0)))
print ("sigmoid(9.2) = " + str(sigmoid(9.2)))打印结果
sigmoid(0) = 0.5
sigmoid(9.2) = 0.999898970806
实现一个初始化参数w( 初始化为 dim维值为0的向量)和b(初始化为0)的函数
def initialize_with_zeros(dim):
"""
此函数为w创建一个维度为(dim,1)的0向量,并将b初始化为0。
参数:
dim - 我们想要的w矢量的大小(或者这种情况下的参数数量)
返回:
w - 维度为(dim,1)的初始化向量。
b - 初始化的标量(对应于偏差)
"""
w = np.zeros(shape = (dim,1))
b = 0
return (w , b)实现一个计算成本函数及其渐变的梯度函数,参考如下公式
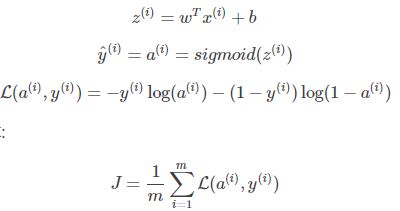
def propagate(w, b, X, Y):
"""
实现前向和后向传播的成本函数及其梯度。
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 矩阵类型为(num_px * num_px * 3,训练数量)
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据数量)
返回:
cost- 逻辑回归的负对数似然成本
dw - 相对于w的损失梯度
db - 相对于b的损失梯度
"""
m = X.shape[1]
#####正向传播 ,计算当前损失#####
#计算激活值,公式sigmoid(w ^ T x + b)
A = sigmoid(np.dot(w.T,X) + b)
#计算成本,参考上图公式
cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A)))
#####反向传播,求偏导数,计算当前梯度#####
dw = (1 / m) * np.dot(X, (A - Y).T) #请参考视频中的偏导公式。
db = (1 / m) * np.sum(A - Y) #请参考视频中的偏导公式。
cost = np.squeeze(cost)
assert(cost.shape == ())
#创建一个字典,把dw和db保存起来。
grads = {
"dw": dw,
"db": db
}
return (grads , cost)测试结果:
====================测试propagate====================
dw = [[ 0.99993216]
[ 1.99980262]]
db = 0.499935230625
cost = 6.00006477319实现一个optimize 函数, 通过最小化成本函数J 来学习 w和b ,
步骤:
- 计算 Y^=A=σ(wTX+b)Y^=A=σ(wTX+b)
- 将a的值变为0(如果激活值<= 0.5)或者为1(如果激活值> 0.5),
def optimize(w , b , X , Y , num_iterations , learning_rate , print_cost = False):
"""
此函数通过运行梯度下降算法来优化w和b
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数组。
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
num_iterations - 优化循环的迭代次数
learning_rate - 梯度下降更新规则的学习率
print_cost - 每100步打印一次损失值
返回:
params - 包含权重w和偏差b的字典
grads - 包含权重和偏差相对于成本函数的梯度的字典
成本 - 优化期间计算的所有成本列表,将用于绘制学习曲线。
提示:
我们需要写下两个步骤并遍历它们:
1)计算当前参数的成本和梯度,使用propagate()。
2)使用w和b的梯度下降法则更新参数。
"""
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b, X, Y)
dw = grads["dw"]
db = grads["db"]
w = w - learning_rate * dw
b = b - learning_rate * db
#记录成本
if i % 100 == 0:
costs.append(cost)
#打印成本数据
if (print_cost) and (i % 100 == 0):
print("迭代的次数: %i , 误差值: %f" % (i,cost))
params = {
"w" : w,
"b" : b }
grads = {
"dw": dw,
"db": db }
return (params , grads , costs)
#测试optimize
print("====================测试optimize====================")
w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1,2], [3,4]]), np.array([[1, 0]])
params , grads , costs = optimize(w , b , X , Y , num_iterations=100 , learning_rate = 0.009 , print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))打印结果
====================测试optimize====================
w = [[ 0.1124579 ]
[ 0.23106775]]
b = 1.55930492484
dw = [[ 0.90158428]
[ 1.76250842]]
db = 0.430462071679定义二元分类(逻辑回归)预测函数,并把预测值保存在向量Y_prediction中
def predict(w , b , X ):
"""
使用学习逻辑回归参数logistic (w,b)预测标签是0还是1,
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数据
返回:
Y_prediction - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
"""
m = X.shape[1] #图片的数量
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0],1)
#计预测猫在图片中出现的概率
A = sigmoid(np.dot(w.T , X) + b)
for i in range(A.shape[1]):
#将概率a [0,i]转换为实际预测p [0,i]
Y_prediction[0,i] = 1 if A[0,i] > 0.5 else 0
#使用断言
assert(Y_prediction.shape == (1,m))
return Y_prediction
#测试predict
print("====================测试predict====================")
w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1,2], [3,4]]), np.array([[1, 0]])
print("predictions = " + str(predict(w, b, X)))把这些函数统统整合到一个model()函数中
def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
"""
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train - numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train - numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test - numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test - numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations - 表示用于优化参数的迭代次数的超参数
learning_rate - 表示optimize()更新规则中使用的学习速率的超参数
print_cost - 设置为true以每100次迭代打印成本
返回:
d - 包含有关模型信息的字典。
"""
w , b = initialize_with_zeros(X_train.shape[0])
parameters , grads , costs = optimize(w , b , X_train , Y_train,num_iterations , learning_rate , print_cost)
#从字典“参数”中检索参数w和b
w , b = parameters["w"] , parameters["b"]
#预测测试/训练集的例子
Y_prediction_test = predict(w , b, X_test)
Y_prediction_train = predict(w , b, X_train)
#打印训练后的准确性
print("训练集准确性:" , format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100) ,"%")
print("测试集准确性:" , format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100) ,"%")
d = {
"costs" : costs,
"Y_prediction_test" : Y_prediction_test,
"Y_prediciton_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations" : num_iterations }
return d
print("====================测试model====================")
#这里加载的是真实的数据,请参见上面的代码部分。
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)打印结果
====================测试model====================
迭代的次数: 0 , 误差值: 0.693147
迭代的次数: 100 , 误差值: 0.584508
迭代的次数: 200 , 误差值: 0.466949
迭代的次数: 300 , 误差值: 0.376007
迭代的次数: 400 , 误差值: 0.331463
迭代的次数: 500 , 误差值: 0.303273
….
迭代的次数: 1900 , 误差值: 0.140872
训练集准确性: 99.04306220095694 %
测试集准确性: 70.0 %
所以图像识别没有用CNN也可以??个人理解 这个案例大概就是没有经过卷积核提取特征,而把图片所有像素flat成一维向量做2元分类,相当于input 直接进入全连接层 再做2元分类训练;这样做的后果就是计算量比CNN方式较大而已,只要数据集够大,也许不会影响模型预测效果
###########################################################
平面数据分类
如果对一些非线性的2维离散点做2元分类,使用什么算法能比较好的拟合出一个模型?比如下面这个数据集属于非线性分类样本集,如图示:
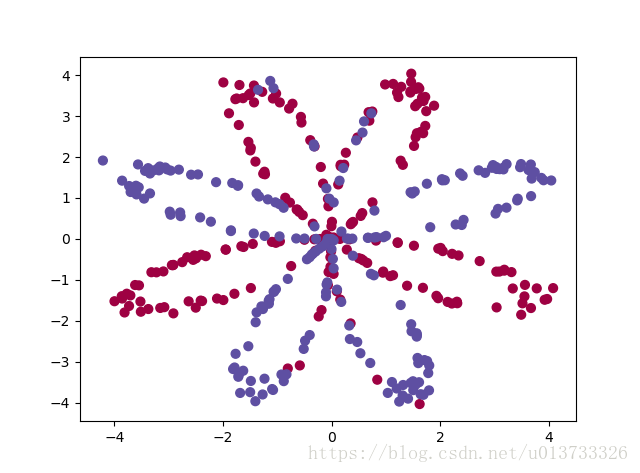
使用sklearn的内置函数 简单的Logistic回归的分类效果不太好,
逻辑回归的准确性只有 47 % , 属于线性不可分的数据集(逻辑回归只适合处理线性可分的数据集?)
X, Y = load_planar_dataset()shape_X = X.shape
shape_Y = Y.shape
m = Y.shape[1] # 训练集里面的数量
print ("X的维度为: " + str(shape_X))
print ("Y的维度为: " + str(shape_Y))
print ("数据集里面的数据有:" + str(m) + " 个")
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T,Y.T)
plot_decision_boundary(lambda x: clf.predict(x), X, Y) #绘制决策边界
plt.title("Logistic Regression") #图标题
LR_predictions = clf.predict(X.T) #预测结果
print ("逻辑回归的准确性: %d " % float((np.dot(Y, LR_predictions) +
np.dot(1 - Y,1 - LR_predictions)) / float(Y.size) * 100) +
"% " + "(正确标记的数据点所占的百分比)")改用神经网络实现该数据集的分类, 只要隐含层神经元足够多, 神经网络 就具有模拟任意复杂非线性映射的能力 ( 神经网络中每一个神经元都可以看作是一个逻辑回归模型,N层神经网络就是N层逻辑回归模型的复合,只是不像逻辑回归中只有一个神经元,一般输入层和隐藏层都是具有多个神经元,而输出层对应一个logistic回归单元或者softmax单元,或者一个线性回归模型 ),我们构建如下只有一个隐藏层的浅层NN网络:
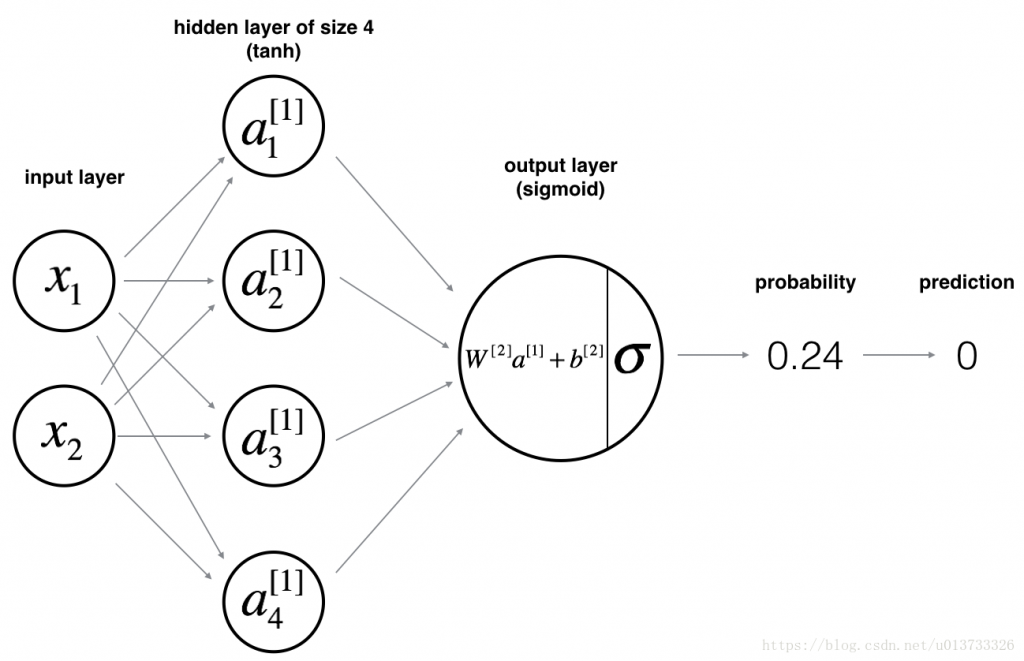
搭建NN网络步骤:
- 定义神经网络结构(输入单元的数量,隐藏单元的数量等)。
- 初始化模型的参数
- 循环:
实施前向传播
计算损失
实现向后传播
更新参数(梯度下降)
定义神经网络结构的函数
def layer_sizes(X , Y):
"""
参数:
X - 输入数据集,维度为(输入的数量,训练/测试的数量)
Y - 标签,维度为(输出的数量,训练/测试数量)
返回:
n_x - 输入层的数量
n_h - 隐藏层的数量
n_y - 输出层的数量
"""
n_x = X.shape[0] #输入层
n_h = 4 #,隐藏层,硬编码为4
n_y = Y.shape[0] #输出层
return (n_x,n_h,n_y)
#测试layer_sizes
print("=========================测试layer_sizes=========================")
X_asses , Y_asses = layer_sizes_test_case()
(n_x,n_h,n_y) = layer_sizes(X_asses,Y_asses)
print("输入层的节点数量为: n_x = " + str(n_x))
print("隐藏层的节点数量为: n_h = " + str(n_h))
print("输出层的节点数量为: n_y = " + str(n_y))=========================测试layer_sizes========================= 输入层的节点数量为: n_x = 5
隐藏层的节点数量为: n_h = 4
输出层的节点数量为: n_y = 2
定义初始化模型参数的函数
def initialize_parameters( n_x , n_h ,n_y):
"""
参数:
n_x - 输入层节点的数量
n_h - 隐藏层节点的数量
n_y - 输出层节点的数量
返回:
parameters - 包含参数的字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
np.random.seed(2) #指定一个随机种子
#隐藏层FP的参数初始化
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
#输出层FP的参数初始化
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
#使用断言确保我的数据格式是正确的
assert(W1.shape == ( n_h , n_x ))
assert(b1.shape == ( n_h , 1 ))
assert(W2.shape == ( n_y , n_h ))
assert(b2.shape == ( n_y , 1 ))
parameters = {"W1" : W1,
"b1" : b1,
"W2" : W2,
"b2" : b2 }
return parameters定义前向传播FP函数
def forward_propagation( X , parameters ):
"""
参数:
X - 维度为(n_x,m)的输入数据。
parameters - 初始化函数(initialize_parameters)的输出
返回:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型变量
"""
#使用字典类型的parameters(它是initialize_parameters() 的输出)检索每个参数
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
#实现向前传播
#隐藏层假设函数输出
Z1 = np.dot(W1 , X) + b1
#隐藏层激活函数结果
A1 = np.tanh(Z1)
#输出层计算假设函数输出
Z2 = np.dot(W2 , A1) + b2
#输出层计算激活函数结果
A2 = sigmoid(Z2)
#
assert(A2.shape == (1,X.shape[1]))
#反向传播所需的值存储在“cache”中,cache将作为反向传播函数的输入
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return (A2, cache)定义损失函数 : 交叉损失(逻辑分类用)
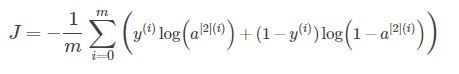
def compute_cost(A2,Y,parameters):
"""
计算交叉熵成本,
参数:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
Y - "True"标签向量,维度为(1,数量)
parameters - 一个包含W1,B1,W2和B2的字典类型的变量
返回:
成本 - 交叉熵成本给出方程(13)
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
#计算成本
logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
cost = - np.sum(logprobs) / m
cost = float(np.squeeze(cost))
assert(isinstance(cost,float))
return cost定义BP向后传播函数
参考公式

怎么推导出来的?(偏导数+ 链式求导 )
反向传播第二层的偏导数推导如下:
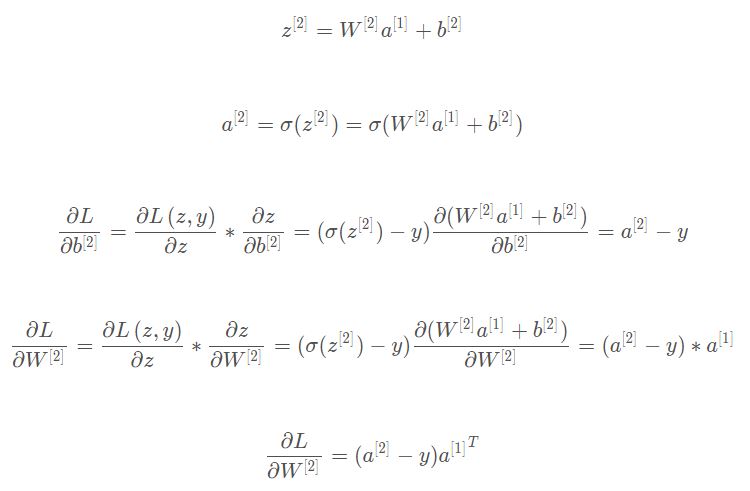
反向传播的第一层的偏导数:
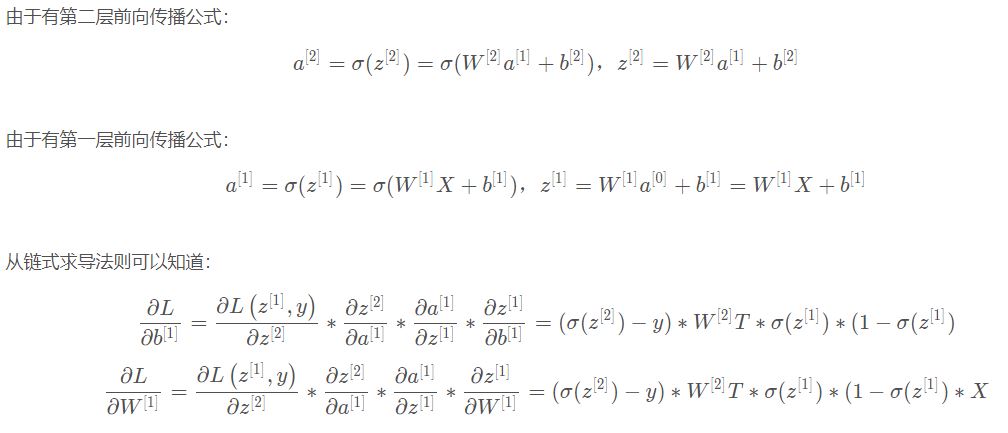
结合导数基础公式推导


代码实现
def backward_propagation(parameters,cache,X,Y):
"""
使用上述说明搭建反向传播函数。
参数:
parameters - 包含我们的参数的一个字典类型的变量。
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型的变量。
X - 输入数据,维度为(2,数量)
Y - “True”标签,维度为(1,数量)
返回:
grads - 包含W和b的导数一个字典类型的变量。
"""
m = X.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2= A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2 }
return grads定义梯度下降函数

def update_parameters(parameters,grads,learning_rate=1.2):
"""
使用上面给出的梯度下降更新规则更新参数
参数:
parameters - 包含参数的字典类型的变量。
grads - 包含导数值的字典类型的变量。
learning_rate - 学习速率
返回:
parameters - 包含更新参数的字典类型的变量。
"""
W1,W2 = parameters["W1"],parameters["W2"]
b1,b2 = parameters["b1"],parameters["b2"]
dW1,dW2 = grads["dW1"],grads["dW2"]
db1,db2 = grads["db1"],grads["db2"]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters定义模型训练全流程函数
def nn_model(X,Y,n_h,num_iterations,print_cost=False):
"""
参数:
X - 数据集,维度为(2,示例数)
Y - 标签,维度为(1,示例数)
n_h - 隐藏层的数量
num_iterations - 梯度下降循环中的迭代次数
print_cost - 如果为True,则每1000次迭代打印一次成本数值
返回:
parameters - 模型学习的参数,它们可以用来进行预测。
"""
np.random.seed(3) #指定随机种子
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x,n_h,n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
for i in range(num_iterations):
A2 , cache = forward_propagation(X,parameters)
cost = compute_cost(A2,Y,parameters)
grads = backward_propagation(parameters,cache,X,Y)
parameters = update_parameters(parameters,grads,learning_rate = 0.5)
if print_cost:
if i%1000 == 0:
print("第 ",i," 次循环,成本为:"+str(cost))
return parameters定义训练函数
def predict(parameters,X):
"""
使用学习的参数,为X中的每个示例预测一个类
参数:
parameters - 包含参数的字典类型的变量。
X - 输入数据(n_x,m)
返回
predictions - 我们模型预测的向量(红色:0 /蓝色:1)
"""
A2 , cache = forward_propagation(X,parameters)
predictions = np.round(A2)
return predictions正式运行
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True)
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')执行结果打印
第 0 次循环,成本为:0.6930480201239823
第 1000 次循环,成本为:0.28808329356901835
第 2000 次循环,成本为:0.25438549407324496
第 3000 次循环,成本为:0.23386415038952196
第 4000 次循环,成本为:0.22679248744854008
第 5000 次循环,成本为:0.22264427549299015
第 6000 次循环,成本为:0.21973140404281316
第 7000 次循环,成本为:0.21750365405131294
第 8000 次循环,成本为:0.21950396469467315
第 9000 次循环,成本为:0.2185709575018246
准确率: 90%更改隐藏层节点数量会对精准度的影响如何?
上面的实验把隐藏层定为4个节点,现在我们更改隐藏层里面的节点数量,看一看节点数量是否会对结果造成影响
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50] #隐藏层数量
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i + 1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations=5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
print ("隐藏层的节点数量: {} ,准确率: {} %".format(n_h, accuracy))测试结果看隐藏节数总体上看是越多,准确率越高(需要考虑计算量和准确率的平衡):
隐藏层的节点数量: 1 ,准确率: 67.5 %
隐藏层的节点数量: 2 ,准确率: 67.25 %
隐藏层的节点数量: 3 ,准确率: 90.75 %
隐藏层的节点数量: 4 ,准确率: 90.5 %
隐藏层的节点数量: 5 ,准确率: 91.25 %
隐藏层的节点数量: 20 ,准确率: 90.0 %
#######搭建多层神经网络以及应用
步骤:
1初始化网络参数
2前向传播
2.1 计算一层的中线性求和的部分
2.2 计算激活函数的部分(ReLU使用L-1次,Sigmod使用1次)
2.3 结合线性求和与激活函数
3计算误差
4反向传播
4.1 线性部分的反向传播公式
4.2 激活函数部分的反向传播公式
4.3 结合线性部分与激活函数的反向传播公式
5更新参数
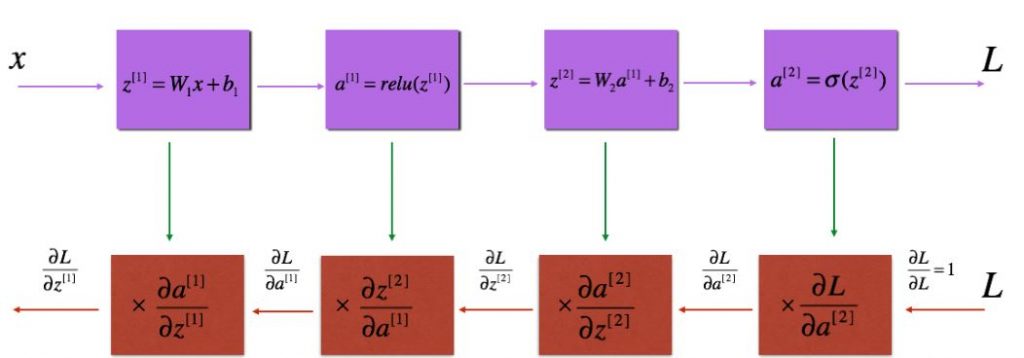
一个L层的神经网络而言,初始化会是什么样的?
假设X(输入数据)的维度为(12288,209):
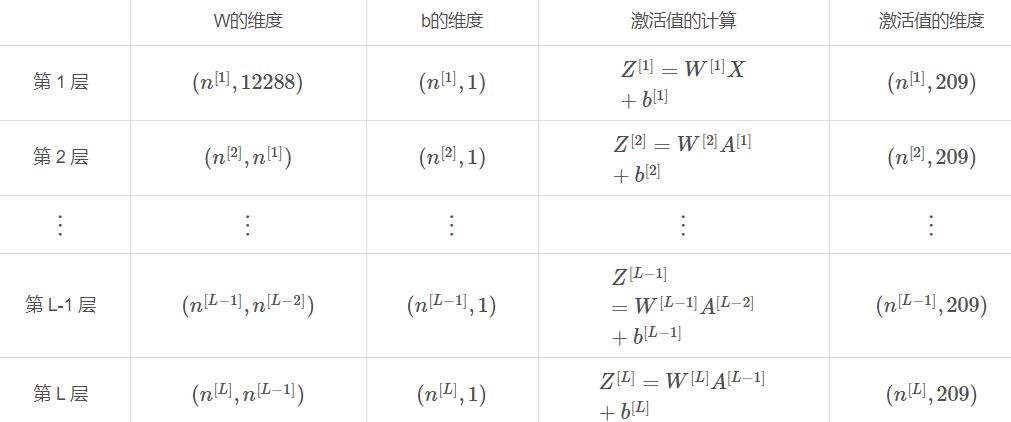
第一个隐藏层中的每个神经元节点将执行相同的计算。 所以即使经过多次梯度下降迭代后,层中的每个神经元节点都会计算出与其他神经元节点相同的东西
np.random.randn(..,..)/ XX 将权重初始化为相对较小的值,是输入到激活函数中的值比较小,梯度值不容易出现接近为0的情况 , 从而 优化算法也不会因此变得缓慢
- 不同的初始化方法可能导致性能最终不同
- 随机初始化有助于打破对称,使得不同隐藏层的单元可以学习到不同的参数。
- 初始化时,初始值不宜过大。
- 初始化搭配ReLU激活函数常常可以得到不错的效果。
def initialize_parameters_deep(layers_dims):
"""
此函数是为了初始化多层网络参数而使用的函数。
参数:
layers_dims - 包含我们网络中每个图层的节点数量的列表
返回:
parameters - 包含参数“W1”,“b1”,...,“WL”,“bL”的字典:
W1 - 权重矩阵,维度为(layers_dims [1],layers_dims [1-1])
bl - 偏向量,维度为(layers_dims [1],1)
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for l in range(1,L):
parameters["W" + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) / np.sqrt(layers_dims[l - 1])
parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))
#确保我要的数据的格式是正确的
assert(parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l-1]))
assert(parameters["b" + str(l)].shape == (layers_dims[l], 1))
return parameters前向传播函数
三个步骤:
1 LINEAR
2 LINEAR - >ACTIVATION,其中激活函数将会使用ReLU或Sigmoid。
3 [LINEAR - > RELU] ×(L-1) - > LINEAR - > SIGMOID(整个模型)LINEAR部分代码实现:
def linear_forward(A,W,b):
"""
实现前向传播的线性部分。
参数:
A - 来自上一层(或输入数据)的激活,维度为(上一层的节点数量,示例的数量)
W - 权重矩阵,numpy数组,维度为(当前图层的节点数量,前一图层的节点数量)
b - 偏向量,numpy向量,维度为(当前图层节点数量,1)
返回:
Z - 激活功能的输入,也称为预激活参数
cache - 一个包含“A”,“W”和“b”的字典,存储这些变量以有效地计算后向传递
"""
Z = np.dot(W,A) + b
assert(Z.shape == (W.shape[0],A.shape[1]))
cache = (A,W,b)
return Z,cache激活函数部分
def linear_activation_forward(A_prev,W,b,activation):
"""
实现LINEAR-> ACTIVATION 这一层的前向传播
参数:
A_prev - 来自上一层(或输入层)的激活,维度为(上一层的节点数量,示例数)
W - 权重矩阵,numpy数组,维度为(当前层的节点数量,前一层的大小)
b - 偏向量,numpy阵列,维度为(当前层的节点数量,1)
activation - 选择在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
A - 激活函数的输出,也称为激活后的值
cache - 一个包含“linear_cache”和“activation_cache”的字典,我们需要存储它以有效地计算后向传递
"""
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
assert(A.shape == (W.shape[0],A_prev.shape[1]))
cache = (linear_cache,activation_cache)
return A,cache三个步骤来构建反向传播 函数:
- LINEAR 后向计算
- LINEAR -> ACTIVATION 后向计算,其中ACTIVATION 计算Relu或者Sigmoid 的结果
- [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID 后向计算 (整个模型)
相关公式
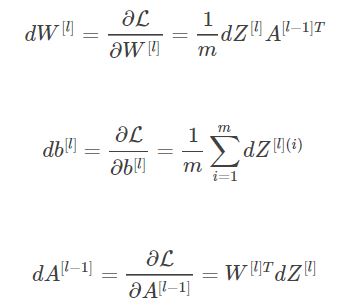
def linear_backward(dZ,cache):
"""
为单层实现反向传播的线性部分(第L层)
参数:
dZ - 相对于(当前第l层的)线性输出的成本梯度
cache - 来自当前层前向传播的值的元组(A_prev,W,b)
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度,与W的维度相同
db - 相对于b(当前层l)的成本梯度,与b维度相同
"""
A_prev, W, b = cache
m = A_prev.shape[1]
dW = np.dot(dZ, A_prev.T) / m
db = np.sum(dZ, axis=1, keepdims=True) / m
dA_prev = np.dot(W.T, dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db定义BP线性激活部分
参考公式:
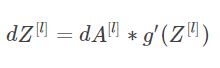
def linear_activation_backward(dA,cache,activation="relu"):
"""
实现LINEAR-> ACTIVATION层的后向传播。
参数:
dA - 当前层l的激活后的梯度值
cache - 我们存储的用于有效计算反向传播的值的元组(值为linear_cache,activation_cache)
activation - 要在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度值,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度值,与W的维度相同
db - 相对于b(当前层l)的成本梯度值,与b的维度相同
"""
linear_cache, activation_cache = cache
if activation == "relu":
#relu_backward: 实现了relu()函数的反向传播
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
#sigmoid_backward:实现了sigmoid()函数的反向传播
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev,dW,db构建多层模型向后传播函数
def L_model_backward(AL,Y,caches):
"""
对[LINEAR-> RELU] *(L-1) - > LINEAR - > SIGMOID组执行反向传播,就是多层网络的向后传播
参数:
AL - 概率向量,正向传播的输出(L_model_forward())
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
caches - 包含以下内容的cache列表:
linear_activation_forward("relu")的cache,不包含输出层
linear_activation_forward("sigmoid")的cache
返回:
grads - 具有梯度值的字典
grads [“dA”+ str(l)] = ...
grads [“dW”+ str(l)] = ...
grads [“db”+ str(l)] = ...
"""
grads = {}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache = caches[L-1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, "sigmoid")
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, "relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads梯度下降更新参数
def update_parameters(parameters, grads, learning_rate):
"""
使用梯度下降更新参数
参数:
parameters - 包含你的参数的字典
grads - 包含梯度值的字典,是L_model_backward的输出
返回:
parameters - 包含更新参数的字典
参数[“W”+ str(l)] = ...
参数[“b”+ str(l)] = ...
"""
L = len(parameters) // 2 #整除
for l in range(L):
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters 开始构建两层的神经网络 :
INPUT -> LINEAR -> RELU -> LINEAR -> SIGMOID -> OUTPUT
def two_layer_model(X,Y,layers_dims,learning_rate=0.0075,num_iterations=3000,print_cost=False,isPlot=True):
"""
实现一个两层的神经网络,【LINEAR->RELU】 -> 【LINEAR->SIGMOID】
参数:
X - 输入的数据,维度为(n_x,例子数)
Y - 标签,向量,0为非猫,1为猫,维度为(1,数量)
layers_dims - 层数的向量,维度为(n_y,n_h,n_y)
learning_rate - 学习率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每100次打印一次
isPlot - 是否绘制出误差值的图谱
返回:
parameters - 一个包含W1,b1,W2,b2的字典变量
"""
np.random.seed(1)
grads = {}
costs = []
(n_x,n_h,n_y) = layers_dims
"""
初始化参数
"""
parameters = initialize_parameters(n_x, n_h, n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
"""
开始进行迭代
"""
for i in range(0,num_iterations):
#前向传播
A1, cache1 = linear_activation_forward(X, W1, b1, "relu")
A2, cache2 = linear_activation_forward(A1, W2, b2, "sigmoid")
#计算成本
cost = compute_cost(A2,Y)
#后向传播
##初始化后向传播
dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
##向后传播,输入:“dA2,cache2,cache1”。 输出:“dA1,dW2,db2;还有dA0(未使用),dW1,db1”。
dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
##向后传播完成后的数据保存到grads
grads["dW1"] = dW1
grads["db1"] = db1
grads["dW2"] = dW2
grads["db2"] = db2
#更新参数
parameters = update_parameters(parameters,grads,learning_rate)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
#打印成本值,如果print_cost=False则忽略
if i % 100 == 0:
#记录成本
costs.append(cost)
#是否打印成本值
if print_cost:
print("第", i ,"次迭代,成本值为:" ,np.squeeze(cost))
#迭代完成,根据条件绘制图
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
#返回parameters
return parameters数据集加载,开始正式训练2层NN网络
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()
train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y
n_x = 12288
n_h = 7
n_y = 1
layers_dims = (n_x,n_h,n_y)
parameters = two_layer_model(train_x, train_set_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True,isPlot=True)打印结果
第 0 次迭代,成本值为: 0.69304973566
第 100 次迭代,成本值为: 0.646432095343
第 200 次迭代,成本值为: 0.632514064791
第 300 次迭代,成本值为: 0.601502492035
…
第 2000 次迭代,成本值为: 0.0743907870432
第 2100 次迭代,成本值为: 0.0663074813227
第 2200 次迭代,成本值为: 0.0591932950104
第 2300 次迭代,成本值为: 0.0533614034856
搭建多层神经网络
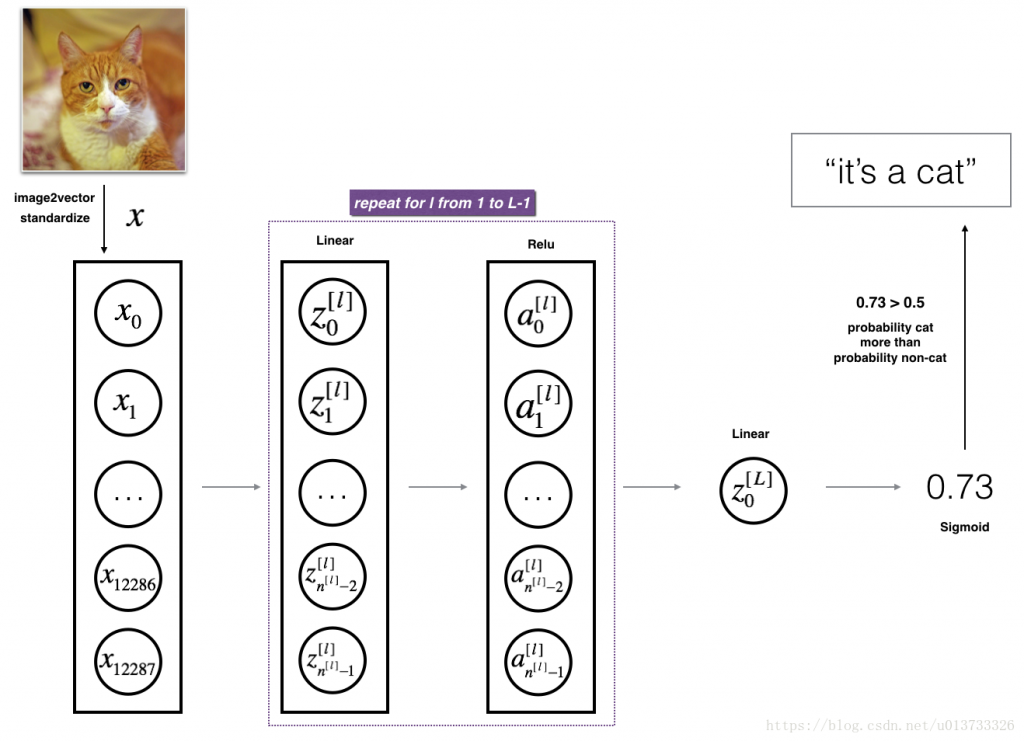
定义 多层模型的前向传播计算模型 函数
def L_model_backward(AL,Y,caches):
"""
实现[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID计算前向传播,也就是多层网络的前向传播,为后面每一层都执行LINEAR和ACTIVATION
参数:
X - 数据,numpy数组,维度为(输入节点数量,示例数)
parameters - initialize_parameters_deep()的输出
返回:
AL - 最后的激活值
caches - 包含以下内容的缓存列表:
linear_relu_forward()的每个cache(有L-1个,索引为从0到L-2)
linear_sigmoid_forward()的cache(只有一个,索引为L-1)
"""
caches = []
A = X
L = len(parameters) // 2
for l in range(1,L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], "relu")
caches.append(cache)
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
caches.append(cache)
assert(AL.shape == (1,X.shape[1]))
return AL,cachesdef L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False,isPlot=True):
"""
实现一个L层神经网络:[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID。
参数:
X - 输入的数据,维度为(n_x,例子数)
Y - 标签,向量,0为非猫,1为猫,维度为(1,数量)
layers_dims - 层数的向量,维度为(n_y,n_h,···,n_h,n_y)
learning_rate - 学习率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每100次打印一次
isPlot - 是否绘制出误差值的图谱
返回:
parameters - 模型学习的参数。 然后他们可以用来预测。
"""
np.random.seed(1)
costs = []
parameters = initialize_parameters_deep(layers_dims)
for i in range(0,num_iterations):
AL , caches = L_model_forward(X,parameters)
cost = compute_cost(AL,Y)
grads = L_model_backward(AL,Y,caches)
parameters = update_parameters(parameters,grads,learning_rate)
#打印成本值,如果print_cost=False则忽略
if i % 100 == 0:
#记录成本
costs.append(cost)
#是否打印成本值
if print_cost:
print("第", i ,"次迭代,成本值为:" ,np.squeeze(cost))
#迭代完成,根据条件绘制图
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameterstrain_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()
train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y
layers_dims = [12288, 20, 7, 5, 1] # 5-layer model
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True,isPlot=True)部分打印结果
第 2100 次迭代,成本值为: 0.0575839119861
第 2200 次迭代,成本值为: 0.044567534547
第 2300 次迭代,成本值为: 0.038082751666
第 2400 次迭代,成本值为: 0.0344107490184########################推导BP算法#################
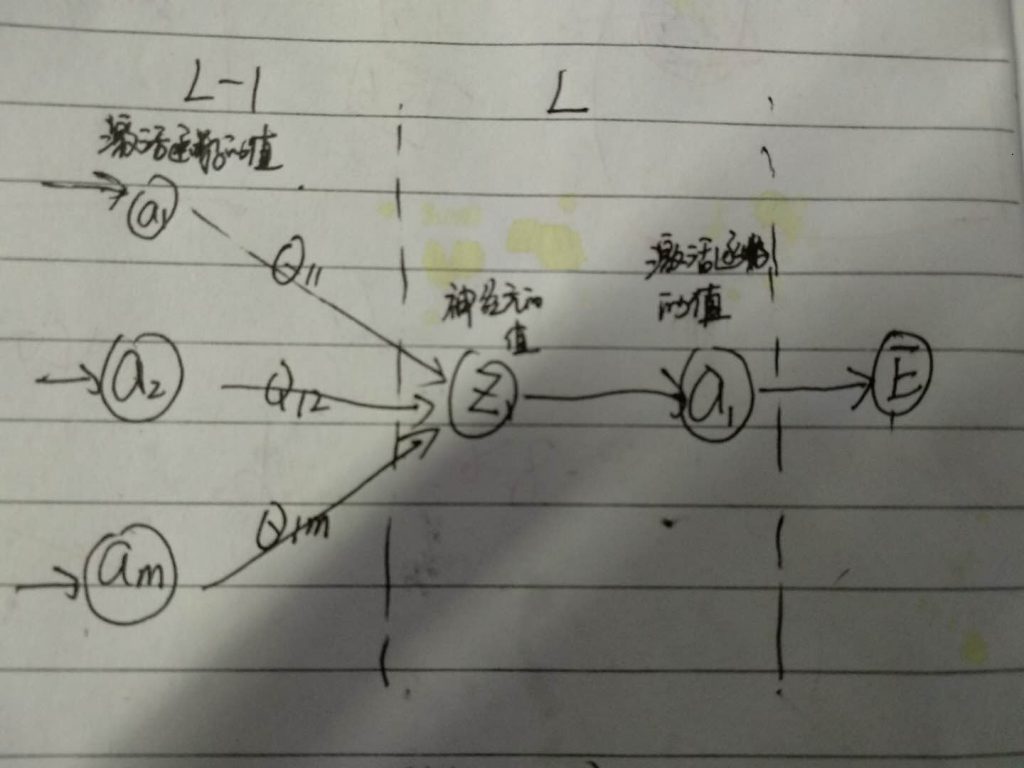

f'(Z (L)) 表示对L层的激活函数求导数
线性回归和逻辑回归的差异是什么?
1. 前者输出的是连续值,后者输出的是离散值 ;
2.线性回归 由input+ 假设函数(N元M次函数) 组成, 逻辑回归由input + (假设函数+ 非线性激活函数) 组成, 神经网络由 input+ 多层 (假设函数+ 非线性激活函数) [+ 非线性激活函数(分类层)] 组成
#########################################
设计一个模型,可以用于推荐在足球场中守门员将球发至哪个位置可以让本队的球员抢到球的可能性更大
train_X, train_Y, test_X, test_Y = reg_utils.load_2D_dataset(is_plot=True)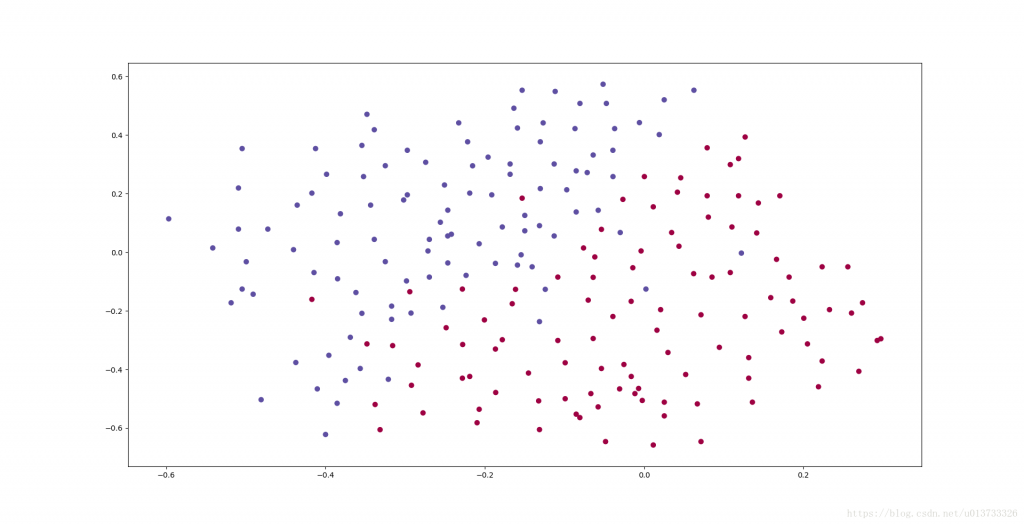
每一个点代表球落下的可能的位置,蓝色代表己方的球员会抢到球,红色代表对手的球员会抢到球,我们要做的就是使用模型来画出一条线,来找到适合我方球员能抢到球的位置 ;
同时对比出不同的模型的优劣:
- 不使用正则化
- 使用正则化 (减少过拟合)
2.1 使用L2正则化
2.2 使用随机节点删除
def model(X,Y,learning_rate=0.3,num_iterations=30000,print_cost=True,is_plot=True,lambd=0,keep_prob=1):
"""
实现一个三层的神经网络:LINEAR ->RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
参数:
X - 输入的数据,维度为(2, 要训练/测试的数量)
Y - 标签,【0(蓝色) | 1(红色)】,维度为(1,对应的是输入的数据的标签)
learning_rate - 学习速率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每迭代10000次打印一次,但是每1000次记录一个成本值
is_polt - 是否绘制梯度下降的曲线图
lambd - 正则化的超参数,实数
keep_prob - 随机删除节点的概率
返回
parameters - 学习后的参数
"""
grads = {}
costs = []
m = X.shape[1]
layers_dims = [X.shape[0],20,3,1]
#初始化参数
parameters = reg_utils.initialize_parameters(layers_dims)
#开始学习
for i in range(0,num_iterations):
#前向传播
##是否随机删除节点
if keep_prob == 1:
###不随机删除节点
a3 , cache = reg_utils.forward_propagation(X,parameters)
elif keep_prob < 1:
###随机删除节点
a3 , cache = forward_propagation_with_dropout(X,parameters,keep_prob)
else:
print("keep_prob参数错误!程序退出。")
exit
#计算成本
## 是否使用二范数
if lambd == 0:
###不使用L2正则化
cost = reg_utils.compute_cost(a3,Y)
else:
###使用L2正则化
cost = compute_cost_with_regularization(a3,Y,parameters,lambd)
#反向传播
##可以同时使用L2正则化和随机删除节点,但是本次实验不同时使用。
assert(lambd == 0 or keep_prob ==1)
##两个参数的使用情况
if (lambd == 0 and keep_prob == 1):
### 不使用L2正则化和不使用随机删除节点
grads = reg_utils.backward_propagation(X,Y,cache)
elif lambd != 0:
### 使用L2正则化,不使用随机删除节点
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
### 使用随机删除节点,不使用L2正则化
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
#更新参数
parameters = reg_utils.update_parameters(parameters, grads, learning_rate)
#记录并打印成本
if i % 1000 == 0:
## 记录成本
costs.append(cost)
if (print_cost and i % 10000 == 0):
#打印成本
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
#是否绘制成本曲线图
if is_plot:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
#返回学习后的参数
return parametersdef forward_propagation_with_dropout(X,parameters,keep_prob=0.5):
"""
实现具有随机舍弃节点的前向传播。
LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
参数:
X - 输入数据集,维度为(2,示例数)
parameters - 包含参数“W1”,“b1”,“W2”,“b2”,“W3”,“b3”的python字典:
W1 - 权重矩阵,维度为(20,2)
b1 - 偏向量,维度为(20,1)
W2 - 权重矩阵,维度为(3,20)
b2 - 偏向量,维度为(3,1)
W3 - 权重矩阵,维度为(1,3)
b3 - 偏向量,维度为(1,1)
keep_prob - 随机删除的概率,实数
返回:
A3 - 最后的激活值,维度为(1,1),正向传播的输出
cache - 存储了一些用于计算反向传播的数值的元组
"""
np.random.seed(1)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
#LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1,X) + b1
A1 = reg_utils.relu(Z1)
#下面的步骤1-4对应于上述的步骤1-4。
D1 = np.random.rand(A1.shape[0],A1.shape[1]) #步骤1:初始化矩阵D1
D1 = D1 < keep_prob #步骤2:将D1的值转换为0或1(使用keep_prob作为阈值)
A1 = A1 * D1 #步骤3:舍弃A1的一些节点(将它的值变为0或False)
A1 = A1 / keep_prob #步骤4:缩放未舍弃的节点(不为0)的值
"""
#不理解的同学运行一下下面代码就知道了。
import numpy as np
np.random.seed(1)
A1 = np.random.randn(1,3)
D1 = np.random.rand(A1.shape[0],A1.shape[1])
keep_prob=0.5
D1 = D1 < keep_prob
print(D1)
A1 = 0.01
A1 = A1 * D1
A1 = A1 / keep_prob
print(A1)
"""
#dropout部分特征后的矩阵再输入到假设函数中
Z2 = np.dot(W2,A1) + b2
A2 = reg_utils.relu(Z2)
#下面的步骤1-4对应于上述的步骤1-4。
D2 = np.random.rand(A2.shape[0],A2.shape[1]) #步骤1:初始化矩阵D2
D2 = D2 < keep_prob #步骤2:将D2的值转换为0或1(使用keep_prob作为阈值)
A2 = A2 * D2 #步骤3:舍弃A1的一些节点(将它的值变为0或False)
A2 = A2 / keep_prob #步骤4:缩放未舍弃的节点(不为0)的值
Z3 = np.dot(W3, A2) + b3
A3 = reg_utils.sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cachedef backward_propagation_with_dropout(X,Y,cache,keep_prob):
"""
实现我们随机删除的模型的后向传播。
参数:
X - 输入数据集,维度为(2,示例数)
Y - 标签,维度为(输出节点数量,示例数量)
cache - 来自forward_propagation_with_dropout()的cache输出
keep_prob - 随机删除的概率,实数
返回:
gradients - 一个关于每个参数、激活值和预激活变量的梯度值的字典
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3,A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2 # 步骤1:使用正向传播期间相同的节点,舍弃那些关闭的节点(因为任何数乘以0或者False都为0或者False)
dA2 = dA2 / keep_prob # 步骤2:缩放未舍弃的节点(不为0)的值
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1 # 步骤1:使用正向传播期间相同的节点,舍弃那些关闭的节点(因为任何数乘以0或者False都为0或者False)
dA1 = dA1 / keep_prob # 步骤2:缩放未舍弃的节点(不为0)的值
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradientsdef compute_cost_with_regularization(A3,Y,parameters,lambd):
"""
实现公式2的L2正则化计算成本
参数:
A3 - 正向传播的输出结果,维度为(输出节点数量,训练/测试的数量)
Y - 标签向量,与数据一一对应,维度为(输出节点数量,训练/测试的数量)
parameters - 包含模型学习后的参数的字典
返回:
cost - 使用公式2计算出来的正则化损失的值
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = reg_utils.compute_cost(A3,Y)
L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)
cost = cross_entropy_cost + L2_regularization_cost
return cost
#当然,因为改变了成本函数,我们也必须改变向后传播的函数, 所有的梯度都必须根据这个新的成本值来计算。
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
实现我们添加了L2正则化的模型的后向传播。
参数:
X - 输入数据集,维度为(输入节点数量,数据集里面的数量)
Y - 标签,维度为(输出节点数量,数据集里面的数量)
cache - 来自forward_propagation()的cache输出
lambda - regularization超参数,实数
返回:
gradients - 一个包含了每个参数、激活值和预激活值变量的梯度的字典
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3,A2.T) + ((lambd * W3) / m )
db3 = (1 / m) * np.sum(dZ3,axis=1,keepdims=True)
dA2 = np.dot(W3.T,dZ3)
dZ2 = np.multiply(dA2,np.int64(A2 > 0))
dW2 = (1 / m) * np.dot(dZ2,A1.T) + ((lambd * W2) / m)
db2 = (1 / m) * np.sum(dZ2,axis=1,keepdims=True)
dA1 = np.dot(W2.T,dZ2)
dZ1 = np.multiply(dA1,np.int64(A1 > 0))
dW1 = (1 / m) * np.dot(dZ1,X.T) + ((lambd * W1) / m)
db1 = (1 / m) * np.sum(dZ1,axis=1,keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients不使用正则化运行模型训练
parameters = model(train_X, train_Y,is_plot=True)
print("训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)打印结果
第0次迭代,成本值为:0.655741252348
第10000次迭代,成本值为:0.163299875257
第20000次迭代,成本值为:0.138516424233
训练集:
Accuracy: 0.947867298578
测试集:
Accuracy: 0.915使用正则化运行模型训练
parameters = model(train_X, train_Y, lambd=0.7,is_plot=True)
print("使用正则化,训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用正则化,测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)打印结果
第0次迭代,成本值为:0.697448449313
第10000次迭代,成本值为:0.268491887328
第20000次迭代,成本值为:0.268091633713
使用正则化,训练集:
Accuracy: 0.938388625592
使用正则化,测试集:
Accuracy: 0.93使用随机删除节点dropout 训练模型:
parameters = model(train_X, train_Y, keep_prob=0.86, learning_rate=0.3,is_plot=True)
print("使用随机删除节点,训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用随机删除节点,测试集:")
reg_utils.predictions_test = reg_utils.predict(test_X, test_Y, parameters)打印结果
第0次迭代,成本值为:0.654391240515
第10000次迭代,成本值为:0.0610169865749
第20000次迭代,成本值为:0.0605824357985
使用随机删除节点,训练集:
Accuracy: 0.928909952607
使用随机删除节点,测试集:
Accuracy: 0.95实验结果证实 正则化和使用dropout确实能减少模型的方差,即过拟合的情况
######################################################
线性回归 和 逻辑回归 模型的损失函数的区别:
- 线性回归模型中的损失函数为平方差损失函数,其是凸函数
- 逻辑回归中,损失函数为交叉熵损失函数,因为对于逻辑回归来说,若是用平方差损失函数,其入参被 sigmod 激活函数处理后,不能保证损失函数是凸函数
############### 卷积神经网络 – 第二周作业 keras 笑脸识别
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = kt_utils load_dataset()
# Normalize image vectors
X_train = X_train_orig/255.
X_test = X_test_orig/255.
# Reshape
Y_train = Y_train_orig.T
Y_test = Y_test_orig.T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
keras快速构建一个CNN网络
def HappyModel(input_shape):
"""
模型大纲
"""
#定义一个tensor的placeholder,维度为input_shape
X_input = Input(input_shape)
#使用0填充:X_input的周围填充0
X = ZeroPadding2D((3,3))(X_input)
# 对X使用 CONV -> BN -> RELU 块
X = Conv2D(32, (7, 7), strides = (1, 1), name = 'conv0')(X)
X = BatchNormalization(axis = 3, name = 'bn0')(X)
X = Activation('relu')(X)
#最大值池化层
X = MaxPooling2D((2,2),name="max_pool")(X)
#降维,矩阵转化为向量 + 全连接层
X = Flatten()(X)
#由于是2元分类,激活函数使用sigmoid 即可,不用softmax激活函数
X = Dense(1, activation='sigmoid', name='fc')(X)
#创建模型,讲话创建一个模型的实体,我们可以用它来训练、测试。
model = Model(inputs = X_input, outputs = X, name='HappyModel')
return model#创建一个模型实体
happy_model = HappyModel(X_train.shape[1:])
#编译模型,梯度下降优化器使用adam, 由于是2元分类问题,因此损失函数使用交叉熵函数binary_crossentropy
happy_model.compile("adam","binary_crossentropy", metrics=['accuracy'])
#训练模型,会花费大约6-10分钟。
happy_model.fit(X_train, Y_train, epochs=40, batch_size=50)
#评估模型
preds = happy_model.evaluate(X_test, Y_test, batch_size=32, verbose=1, sample_weight=None)
print ("误差值 = " + str(preds[0]))
print ("准确度 = " + str(preds[1]))打印结果:
Epoch 38/40
600/600 [==============================] - 10s 17ms/step - loss: 0.0173 - acc: 0.9950
Epoch 39/40
600/600 [==============================] - 14s 23ms/step - loss: 0.0365 - acc: 0.9883
Epoch 40/40
600/600 [==============================] - 12s 19ms/step - loss: 0.0291 - acc: 0.9900
150/150 [==============================] - 3s 21ms/step
误差值 = 0.407454126676
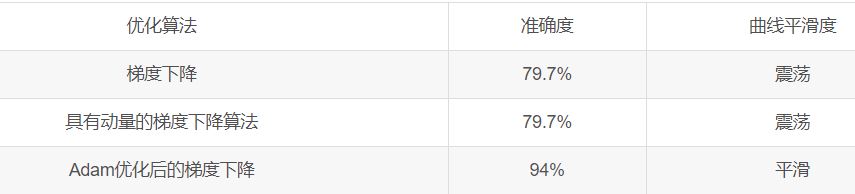
准确度 = 0.840000001589梯度下降优化器 为什么使用adam优化器?
a.收敛得更快 b. 相对较低的内存要求(虽然比梯度下降和动量下降更高)和通常运作良好
##########################################################
卷积神经网络 – 第四周作业 – 人脸识别
使用一个训练好了的模型,该模型使用了“通道优先”的约定来代表卷积网络的激活, 数据的维度是(m,nC,nH,nW)(m,nC,nH,nW)而不是(m,nH,nW,nC)
#获取模型
FRmodel = faceRecoModel(input_shape=(3,96,96))
#打印模型的总参数数量
print("参数数量:" + str(FRmodel.count_params()))定义三元组损失函数
使用三元组图像(A,P,N)(A,P,N)进行训练:
AA是“Anchor”,是一个人的图像。
PP是“Positive”,是相对于“Anchor”的同一个人的另外一张图像。
NN是“Negative”,是相对于“Anchor”的不同的人的另外一张图像。
def triplet_loss(y_true, y_pred, alpha = 0.2):
"""
根据公式(4)实现三元组损失函数
参数:
y_true -- true标签,当你在Keras里定义了一个损失函数的时候需要它,但是这里不需要。
y_pred -- 列表类型,包含了如下参数:
anchor -- 给定的“anchor”图像的编码,维度为(None,128)
positive -- “positive”图像的编码,维度为(None,128)
negative -- “negative”图像的编码,维度为(None,128)
alpha -- 超参数,阈值
返回:
loss -- 实数,损失的值
"""
#获取anchor, positive, negative的图像编码
anchor, positive, negative = y_pred[0], y_pred[1], y_pred[2]
#第一步:计算"anchor" 与 "positive"之间编码的距离,这里需要使用axis=-1
pos_dist = tf.reduce_sum(tf.square(tf.subtract(anchor,positive)),axis=-1)
#第二步:计算"anchor" 与 "negative"之间编码的距离,这里需要使用axis=-1
neg_dist = tf.reduce_sum(tf.square(tf.subtract(anchor,negative)),axis=-1)
#第三步:减去之前的两个距离,然后加上alpha
basic_loss = tf.add(tf.subtract(pos_dist,neg_dist),alpha)
#通过取带零的最大值和对训练样本的求和来计算整个公式
loss = tf.reduce_sum(tf.maximum(basic_loss,0))
return loss加载一个已经训练好了的模型
#开始时间
start_time = time.clock()
#编译模型
FRmodel.compile(optimizer = 'adam', loss = triplet_loss, metrics = ['accuracy'])
#加载权值
fr_utils.load_weights_from_FaceNet(FRmodel)
#结束时间
end_time = time.clock()
#计算时差
minium = end_time - start_time
print("执行了:" + str(int(minium / 60)) + "分" + str(int(minium%60)) + "秒")人脸验证
建一个数据库,里面包含了允许进入的人员的编码向量,我们使用fr_uitls.img_to_encoding(image_path, model)函数来生成编码,它会根据图像来进行模型的前向传播
数 据库使用的是一个字典来表示,这个字典将每个人的名字映射到他们面部的128维编码上
database = {}
database["danielle"] = fr_utils.img_to_encoding("images/danielle.png", FRmodel)
database["younes"] = fr_utils.img_to_encoding("images/younes.jpg", FRmodel)
database["tian"] = fr_utils.img_to_encoding("images/tian.jpg", FRmodel)
database["andrew"] = fr_utils.img_to_encoding("images/andrew.jpg", FRmodel)
database["kian"] = fr_utils.img_to_encoding("images/kian.jpg", FRmodel)
database["dan"] = fr_utils.img_to_encoding("images/dan.jpg", FRmodel)
database["sebastiano"] = fr_utils.img_to_encoding("images/sebastiano.jpg", FRmodel)
database["bertrand"] = fr_utils.img_to_encoding("images/bertrand.jpg", FRmodel)
database["kevin"] = fr_utils.img_to_encoding("images/kevin.jpg", FRmodel)
database["felix"] = fr_utils.img_to_encoding("images/felix.jpg", FRmodel)
database["benoit"] = fr_utils.img_to_encoding("images/benoit.jpg", FRmodel)
database["arnaud"] = fr_utils.img_to_encoding("images/arnaud.jpg", FRmodel)实现 verify() 函数来验证摄像头的照片(image_path)是否与身份证上的名称匹配,这个部分可由以下步骤构成:
根据image_path来计算编码。
计算与存储在数据库中的身份图像的编码的差距。
如果差距小于0.7,那么就打开门,否则就不开门。
def verify(image_path, identity, database, model):
"""
对“identity”与“image_path”的编码进行验证。
参数:
image_path -- 摄像头的图片。
identity -- 字符类型,想要验证的人的名字。
database -- 字典类型,包含了成员的名字信息与对应的编码。
model -- 在Keras的模型的实例。
返回:
dist -- 摄像头的图片与数据库中的图片的编码的差距。
is_open_door -- boolean,是否该开门。
"""
#第一步:计算图像的编码,使用fr_utils.img_to_encoding()来计算。
encoding = fr_utils.img_to_encoding(image_path, model)
#第二步:计算与数据库中保存的编码的差距
dist = np.linalg.norm(encoding - database[identity])
#第三步:判断是否打开门
if dist < 0.7:
print("欢迎 " + str(identity) + "回家!")
is_door_open = True
else:
print("经验证,您与" + str(identity) + "不符!")
is_door_open = False
return dist, is_door_open#网上随便找的图片
img_path = 'images/smile.jpeg'
img = image.load_img(img_path, target_size=(64, 64))
imshow(img)
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
print(happy_model.predict(x))https://github.com/oarriaga/face_classification
没有评论